3月末には収束に向かうと思われたコロナ感染者数が、また増加に向かっている。感染者数の予測においては、京都大学の西浦博教授の試算からSIRモデルへの関心が高くなっている。第4波が予想され、同時にワクチン接種の動きが本格化する現状において、SIRモデルの意義と限界を改めて理解したい。
SIRモデルで感染者数を予測するという試みがなされているが、SIRモデルの予測は、累積の感染者数が1000万人というオーダーにならないかぎり、指数関数と同じ動きをするに過ぎない。日本は、累積の感染者数が1000万人という状況に耐えることができないだろうから、SIRモデルは予測のためには意味のないものだ。
しかし、SIRモデルは、ワクチン接種の劇的な効果を説明することができる。また、イスラエルや米国に匹敵するワープスピードでのワクチン接種が無理であれば、ワクチンと接触減対策をどう組み合わせれば良いかについての理解を与えることができる。ワクチン接種の効果を議論するためにこそSIRモデルを用いるべきだ。
多くの専門家が、SIRモデルは予測のために役に立たず、ワクチンの効果を議論するためにこそ必要だと指摘しないのは不思議である。
直感的説明
SIRモデルについて簡単な算数を用いて説明する前に、直感的説明をしておく。この説明だけ読んでいただければ、算数の部分は読み飛ばしても構わない。
SIRモデルとは、ウイルスの感染力によって、感染者が指数関数的に増加するが、感染者数が増えるほどウイルスの感染力が低下するというモデルだ。なぜそうなるかと言えば、感染して免疫力を持った人は、再び感染することはないからだ。感染者に接触する人が免疫をもっていればそこで感染が遮断される。
1人の感染者が2人に感染させる力を持つウイルスの場合、感染者して免疫を持った人が人口の半分いれば、2人ではなく1人にしか感染する力を持てない。
こうなれば感染が爆発的に増加することはなく、マスクを着けるなど小さな対策で、感染を終息させることができるだろう。しかし、この場合、人口の半分が感染して初めて収束に向かうという話だ。感染者のうち2%の人が死亡するとして、120万人以上の人が死亡するということになる。これは到底採用できない対応策だから、もう少し現実的に考えてみようというのが本稿だ。
SIRモデルとは何か
感染症のSIRモデルというものがある(例えば、桜井進「感染症流行を予測する数理モデル SIR|微分方程式によるシミュレーション」、参照。この説明は微分方程式だが、私の説明は差分方程式となっている)。
SIR のSとは、S(Susceptible)は感染可能性のある人(無免疫者)で、全人口から累積の感染者数(感染経験者数)を引いたものだ。なぜ感染者を引くかと言えば、一度感染した人は免疫を得て再びは感染しないのが通常だからだ(死亡した場合も再びは感染しない)。I(Infected)は感染して回復していない人、R(Recovered)は感染から回復した人だ。途中の式を省略すると(途中の式は付注参照)、
It+1-It=β(St/So)It-γIt (1)
となる。
ここでβは、感染者が1日に移す感染者の数だ。例えば、5日間で2人にうつせば、毎日0.4人ずつうつすことになりβは0.4だ。(St/ So)とは、So 初期の感染可能性のある人(全人口)で現在感染可能性のある人(無免疫者)の数Stを割ったものだ。感染が広まればStは小さくなる。したがって感染する人も少なくなる。
γは感染力のある期間の逆数で、感染力のある期間が5日間であればγ=0.2となる。ここでは、感染力のある期間が終了すれば回復としているが現実にはそう簡単に回復しないという疑問があるかもしれない。疑問は正しいが、このモデルは感染者数がどのように変化するかを問題にしているので、実際に回復しているかどうかはあまり重要ではない。
この式の意味は、感染者の増加数It+1-Itは感染者が1日にうつす感染者の数β(St/S0) Itから回復した感染者の数γItを引いたものになるということである。
ここでβ/γ=R0を基本再生産数という。これは一人の感染者が免疫のある人がいない場合に、何人にうつすかという数だ。β=0.4、γ=0.2であればR0=2であり、2人にうつすということだ。
SIRモデルで感染者数を予測できるか
「SIRモデルで感染者数を予測すると・・・」という記事をよく見るが、私の理解では、SIRモデルは予測のために、なんら役立つものではない。なぜなら、(1)式から
It+1= β(St/So)It-γIt+It
すなわち
It+1/It=〔β(St/So) -γ+1〕 (2)
となるが、Soは日本の人口だから(日本の人口は1億2700万人だが、ここでは簡単のために1億2000万人としておく)、Stが1億1000万、すなわち感染者数の累計が1000万人くらいにならないと感染力を弱める要因にはならないからだ。(St/So)がほぼ1であれば、(2)式は
It+1/It =β-γ+1 (3)
となって、単に指数関数の式にすぎない。βを0.4、γを0.2とすれば
It+1/It=1.2
だ。すなわち、感染者数が20%ずつ増えていくという指数関数にすぎない。もちろん、感染者が1000万人くらいに増えていけば指数関数ではなくなってくるが、感染者1000万人とは死亡率が2%としても20万人が死亡するということになる。そうなれば医療崩壊が起こって治療もできず、死亡率は飛躍的に高まってしまうだろう。つまり、そうなる前に何らかの強力な対策が行われて、再生産数を低める施策が行われるに違いない。
図1は、SIRモデルで感染者数、累積感染者数、無免疫者数(感染可能性のある人)、新規感染者数を示したものだ。β=0.4、γ=0.2の場合を示しているが、新規感染者数(目盛りが右軸にあることに注意)が1日当たり300万人を超えるまでは(累積の感染者経験数が1000万人を超えるまで)1日当たり20%ずつ増加する指数関数とまったく同じ動きをしていることが分かる。新規感染者数が300万人とは考えられない状況だ。すなわち、感染者数が1日、1万人程度では、SIRモデルは指数関数と何ら変わらない。
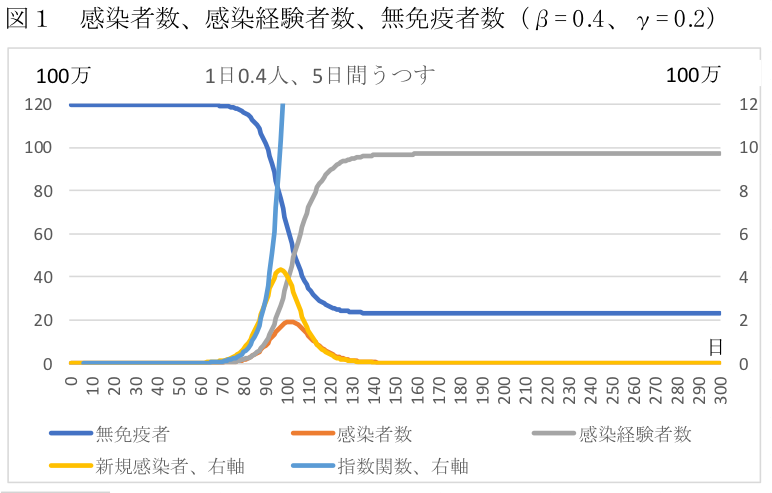
筆者作成
また、β、γは定数ではない。感染が恐ろしければ人は外出を避け、マスクをし、人間とウイルスとの接触を避けるだろう。結果βは小さくなる。また、γは、感染日数の逆数だが、政府が早期に感染者の隔離に成功すれば大きくなる。また、感染者が自らを隔離することでも大きくなるだろう。さらに、SIRモデルからβとγの動きを予測できるものでもない。SIRモデルから分かることはβとγの制御のいずれかが効果的かだが、βとγが完全に独立の事象とも言えない。例えば、感染の疑いのある人が外出を控えればγは上昇するからである。
すなわち、SIRモデルでの予測とは、指数関数の1日当たりの増加率を過去の数字を見ながら適宜操作しているものにすぎない。それは、最も有名になった西浦博北海道大学教授の「『対策何もしないと重篤患者85万人』北大教授試算 『対策で流行止められる』」でも明らかだ。西浦教授は、「新型コロナウイルスの流行対策を何もしないと、国内での重篤患者数が約85万人に上る。また、重篤患者のうちほぼ半数の40万人以上が死亡する」と予測している。これは、何もしないとそうなるという訳で、そうならないように政府の行動が必要であり、また、それほど恐ろしい事態が起きるなら、人々が行動を控えて起きないようにするだろう(むしろ、して下さい)、と言っているに過ぎない。40万人も死亡していないと批判するのは的外れなのだ。
指数関数の恐ろしさとは、新規感染者数が急激に増えることだ。例えば、R0=2の場合、1人の感染者が1万人になるまで51日かかるが、1万人が2万人になるまで4日しかからない。1万人の病床を用意するのに51日かけられるが、あと1万を増やすのは4日間でしなければならない。すなわち、単に指数関数でも、SIRモデルと同じように、早めの対応が必要ということが理解できる。
SIRモデルとコロナワクチン
しかしながら、SIRモデルは予測には役立たないが、ワクチンの効果を認識するためには有効だ。ワクチンとは感染可能性のある人Sを減らすものだからだ。図2は、β=0.4、γ=0.2は同じで、30日後に1日200万回(100万人分)のワープスピードでのワクチン接種をした場合である。ワクチン接種はStを毎日100万人減らすことに相当する(ワクチン接種で感染しなくなる確率は95%だが、ここでは簡単のために100%とした。210万回の接種をすると考えても良い)。その結果、無免疫者数は急減し、累積の感染者数は43万人、1日当たりの新規感染者数はピークで1万人である。しかし、このためにはワクチンを驚くべき速さで接種しないといけない。
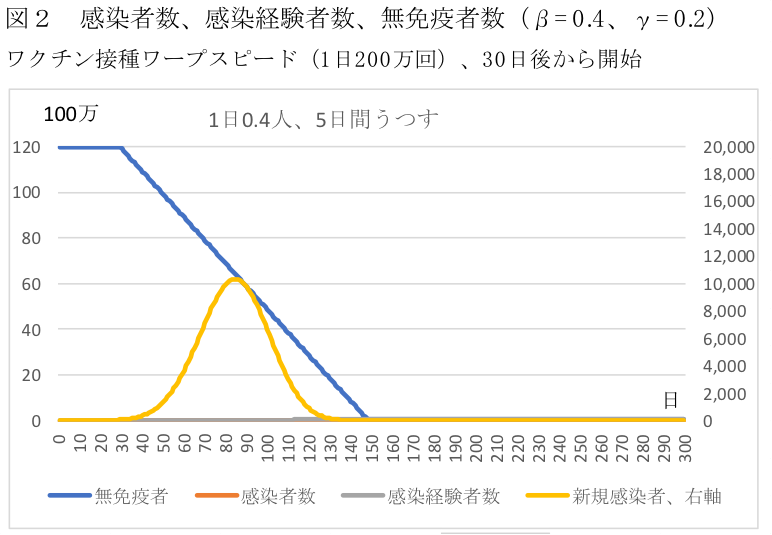
筆者作成
そこで、再生産率の低下とワクチン接種の合わせ技で感染を減らすことを考えよう。β=0.3、γ=0.2と再生産率を1.5として、イスラエルや米国なみのワープスピードの接種は無理と考えて、接種回数を1日50万回(25万人分)と4分の1にする。日本は実は毎年10月から12月中旬までの2.5か月で6000万回のインフルエンザワクチンの接種を行っている。月2400万回、1日80万の接種をしている訳である。ここから考えて1日50万回なら十分可能と考えた。結果は、図3の通りだ。
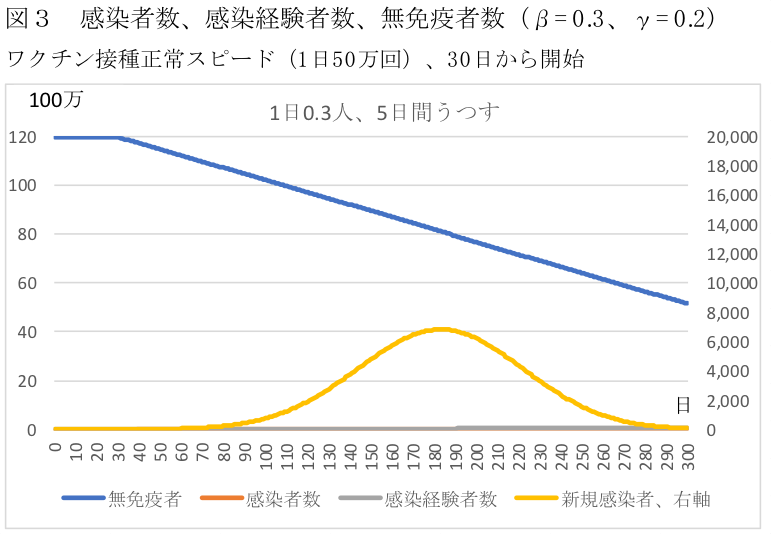
筆者作成
ワクチン接種は無免疫者数Stを毎日25万人減らすことに相当する。その結果、無免疫者数は減少し、累積の感染者数は70万人(死亡率2%として死者1.4万人)、一日当たりの新規感染者数はピークで6800人となる。
再生産数が1よりも小さければ感染症は収束し、1に近ければなかなか増加しない。しかし、私たちが経験したのは、再生産数を1以下にするのは経済的にも精神的にも負担が大きいということであった。それに比べてワクチンは私たちの負担を簡単に低めることができる。しかし、再生産数が大きければ、ワクチンをワープスピードで接種しなければ収束は難しい。平凡な結論だが、可能な限りの低い再生産数と可能な限りの早いワクチン接種がコロナ感染症を収束させるということだ。
β、γ、R0と累積感染者数、新規感染者数の動き
β、γ、R0と感染者数の関係を考えてみたい。図4は、β、γ、R0と累積感染者数、新規感染者数の動きを示したものである。β=0.4、γ=0.2、R0=2の場合、β=0.3、γ=0.
繰り返しになるが、βは感染者が1日に移す感染者の数、γは感染力のある期間の逆数だ。したがってR0=β/γは一人の感染者がうつす人数だ。R0=2、R0=1.5、R0=1.35の場合の感染者数、新規感染者数の動きを見ると、当たり前だが、R0が大きいほど感染者は急激に増加し、小さいほど感染者の増加は抑えられる。R0が2の場合、1億人が感染して初めて感染は収束することになる。R0が1.35の場合は、感染者の増加は長期間抑えられるがそれでもピーク時の1日当たりの新規感染者数は100万人だ。累積の感染者数は最終的には6000万人弱まで上昇する。R0が1.5の場合はこの中間になる。
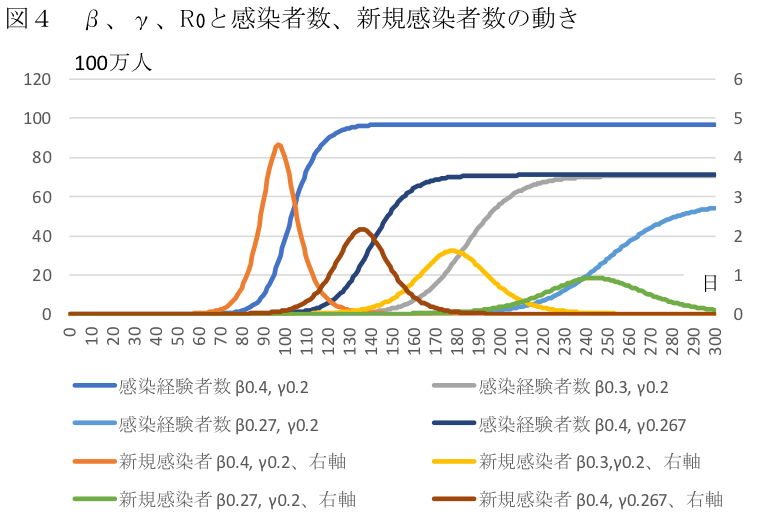
筆者作成
ここで興味深いのはR0が同じ1.5でもβが低下して1.5になった場合と、γが上昇して1.5になった場合では、感染者数、新規感染者数の動きが異なることだ。βが低下して1.5になった場合には、γが上昇する場合に比べて新規感染者の山が遅れ、感染者数の増加も遅れるが、最終的な感染者数は変わらない。一方、γが上昇して1.5になった場合には、新規感染者の山が早くなるが、最終的な感染者数は同じである。最終的な感染者数が同じということは、再生産率が同じなのだから当然でもある。
ではなぜ、βが低下した場合には、新規感染者の山が遅れるのだろうか。前出の(2)式It+1/It=〔β(St/So)It-γ+1〕を見れば分かるように、βが小さく、γが大きくなればIt+1/It、すなわち感染者数の増加率は小さくなる。再生産率が2から1.5になるために、βは0.1低下するが、γは0.067しか上昇していない。すなわち、(St/So)が1に近い場合にはβの低下が大きく影響するが、(St/So)が1からどんどん小さくなるにつれてβ低下の影響が小さくなり、最終的な感染者数は同じになってしまうのだ。
では、βを小さくするのとγを大きくするのとどちらが簡単だろうか。前述のように、βは感染者が1日に移す感染者の数だ。これは人々がマスクを着ける、人ごみに出歩かない、他人と食事をとらないなどの行動をすれば低下する。一方、γは感染力のある期間の逆数だ。感染力のある期間を短くすればγは大きくなるわけだが、感染力のある期間を短くするためには、隔離することだ。濃厚接触者をあぶりだし、あるいは、PCR検査によって感染者を早期に隔離すれば感染期間を短くすることができるだろう(もちろん、すでに述べたようにβとγが完全に独立の事象とも言えないが)。
前者は、政府の注意喚起、実効性のない非常事態宣言でもある程度効果はある。外食産業への休業要請と協力金があればもちろんより効果的になる。後者は行政機構を動かして隔離施設の確保などが必要だ。すると、注意喚起で人々が行動変容をしているうちに、検査体制や隔離施設の拡充などを行うべきだ。現実には、人々の自主的な行動変容の間にγを引き上げる措置が必要だったが、それは不十分だったのではないか。
結論
SIRモデルは、累積の感染者数が1000万人というオーダーにならないかぎり指数関数と同じ動きをするに過ぎない。日本は、累積の感染者数が1000万人という状況に耐えることができないだろうから、SIRモデルは意味のないものだ。
しかし、それでも指数関数の恐ろしさによって早め早めの対応が必要ということを示唆できる。
また、SIRモデルは、人々の行動変容を訴えることで低下させることのできるβと行政的な対応が必要なγをどう組み合わせるべきかについての洞察を得ることができる。
さらに、SIRモデルは、ワクチン接種の劇的な効果を説明することができる。また、イスラエルや米国なみのワープスピードでのワクチン接種が無理であれば、ワクチン接種とウイルスとの接触減対策をどう組み合わせれば良いかについての理解を与えることができる。
付注
本文とやや重なるが、S(Susceptible)は感染可能性のある人(無免疫者)で、全人口から感染者を引いたものだ。I(Infected)は感染して回復していない人、R(Recovered)は感染から回復した人である。
これらから、まず次の式が得られる。
St+1-St=-β*St/So*It (1)
感染した人Iに感染率βをかけた数字がt期の感染者数だ。ここでSt/Soは初期の感染可能性のある人の数(日本の全人口)に対するt期の感染者可能性のある人の数だ。感染率が同じでも、感染可能性のある人の数が減少すれば、感染力は低下することを示している。感染可能性のある人は、感染者が増加すればその分だけ減少することを示している。
Rt+1-Rt=Itγ (2)
γは感染からの回復率なのでItγは回復者数だ。左辺はt+1期の回復者だ。 t時点で無免疫者+感染者+回復者=全人口Nだから
N=St+It+Rt N全人口=一定だから
It=- St-Rt-N (3)
となる。t+1期とt期の差を取ると
It+1-It=-(St+1-St)-(Rt+1-Rt)
これと(1)(2)から
It+1-It=β(St/So)It- Itγ
を得る。







 石田健(イシケン)
石田健(イシケン)














